EXSIM设置

Path Duration

the duration of an EQ signal at hypo-central distance can generally be represented as (according Atkinson and Boore 1995)

$T({R} ) = T{_0} + dR ​$

where $T{_0}​$ is the source duration, and $d​$ is the coefficient controlling the increase of duration with distance; $d​$ is derived empirically. $d​$ may be a single coefficient describing all distances of interest (e.g., Atkinson, 1993b), or it can take different values depending on the distance range(e.g., Atkinson and Boore, 1995). The empirical duration model of Atkinson and Boore (1995) was adopted for this study. The duration increases in a hinged quad linear fashion from the source, mimicking the form of the attenuation model.

$$ T({R}) = T{_0} + dR = \begin{cases} dur(1)(R-0) & 0 \leq R < 10 \\
dur(2)(R-10) & 10 < R \le 70 \\
dur(3)+x(1)(R-70) & 70 < R \le 130 \\
dur(4)+x(2)(R-130) & R > 130
\end{cases}
=\begin{cases} 0 & 0 \le R < 10 \\ 0.16(R-10) & 10 < R \le 70 \\
9.6-0.03(R-70) & 70 < R \le 130 \\ 7.8+0.04(R-130) & R > 130
\end{cases} $$

$x(1) = \frac{9.6-0}{70-10} = 0.16$
$x(2) = \frac{7.8-9.6}{130-70} = -0.03​$

参数文件中设置为:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

if ( subfaultDistance .le. rpathdur(1) ) then
        dur_path = pathdur(1)
else if ( subfaultDistance .ge. rpathdur(ndur_hinges) ) then
        dur_path = pathdur(ndur_hinges) + 
     :     (subfaultDistance - rpathdur(ndur_hinges))*durslope
     :              
else
     call locate(rpathdur, ndur_hinges, subfaultDistance, j)
        dur_path = pathdur(j) + 
     :     (subfaultDistance - rpathdur(j))*( pathdur(j+1)-pathdur(j))
     :              /(rpathdur(j+1)-rpathdur(j))
end if

Geometric spreading

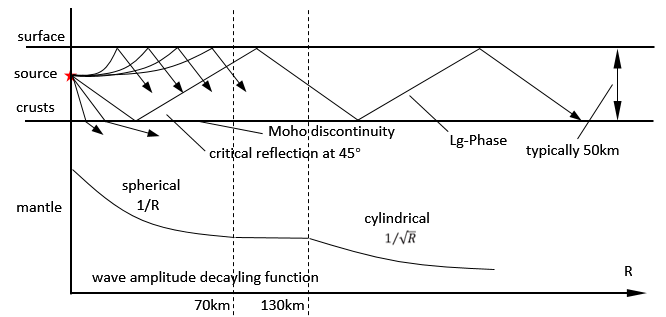
几何扩散一般选用Atkinson和Boore建立的北美东部三段式模型。假设地壳厚度为50km，从震源辐射出的剪切波为球面波，控制着地壳厚度1.4倍（70km）范围内地表的地震动，地震动的傅里叶谱以$1/R$衰减，70km以外，震源辐射的剪切波与从moho面反射的波叠加。在70千米和130千米之间，波的叠加抵消了地震波强度的衰减,几何扩散函数成了一个常数。在130千米之外,地表的地震动受$Lg$波的控制,地震波以柱面波传播,地震动的振幅以$1/ \sqrt{R}​$衰减。

$$ GS({R})=\begin{cases}
R^{-1} &ref \le R < 70 \\ 70^{-1} &70 \le R < 130\\
0.16R^{-0.5} &R \ge 130
\end{cases} $$

为了避免$R​$取到0时，$1/R​$无意义，故设置$R_{ref}=1​$。

Crustal amplification地壳放大因子

指定基于场地土层剖面的基岩放大

对于基岩场地，水平地震动的放大主要是地壳速度结构，和归因于风化岩石层的近地表放大的联合作用。

The amplifications were computed using the square-root impedance (SRI) method (Boore, 2013)(Revisions to some parameters used in stochastic-method simulations of ground motion)

Site mplification Factors Used in the Simulations for NEHRP B/C Boundary (V30=760 m/sec)

Site amplification场地放大因子

H/V ratios

Empirical filter

经验滤波是为了调整震源谱以改变生成的PGA和PSA而设置的，初衷是为了和其他方法计算出的结果匹配来进行比较，实际使用中最好设置为0. (Atkinson. G., K. Goda and K. Assatourians (2011). Comparison of nonlinear structural responses for accelerograms simulated from the stochastic finite-fault approach versus the hybrid broadband approach. Bull. Seism. Soc. Am.,101, 2967-2980)

1
2
3

am3=amplf(f,afreq3,amp3,n_empirical_amps)                     
sig3=amplf(f,afreq3,sigma,n_empirical_amps)                   
sig3=10.**(sig3*ggnqf(iseed)) 

如果第三列是大于1的数，将极大地改变震源谱谱

Pulsing Percent

每个时刻只有有限个子断层破裂，所以使用PulsingPercent参数来平衡能量。