决策树 - AICE's LAB

1.定义

决策树分为分类树和回归树两种，分类树对离散变量做决策树，回归树对连续变量做决策树。
在分类问题中，表示基于特征对实例进行分类的过程。分类决策书是一种描述对实例进行分类的树形结构。决策树由节点（node）和有向边（directed edge）组成。节点的类型有两种：内部节点和叶子节点。其中，内部节点表示一个特征或属性的测试条件（用于分开具有不同特性的记录），叶子节点表示一个分类。
决策树的生成过程主要分为以下3个部分:

特征选择：特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准标准，从而衍生出不同的决策树算法。

决策树生成：根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。树结构来说，递归结构是最容易理解的方式。对应模型的局部选择。

剪枝：决策树容易过拟合，一般来需要剪枝，缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。考虑全局最优。

可以将其看做一个if-then规则的集合。还可以表示为给定特征条件下类的条件概率分布。
决策树学习本质实质是从训练数据集中归纳出一组分类规则。或是指由训练数据集估计条件概率模型。
决策树学习目标用损失函数来表示，通常是正则化的极大似然函数，学习的策略是以损失函数为目标函数的最小化（最优决策树，NP完全问题）。现实中采用启发式方法（近似求解，次最优）。
熵：表示随机变量不确定性的度量。设X是一个取有限个值的离散随机变量，其概率分布为：$P(X=x_i)=pi$，则随机变量X的熵定义为：$H(X)=-\sum^{n}{i=1}{p_ilogpi}$。熵的单位为比特(bit)或纳特(nat)。熵只依赖于X的分布，而与X的取值无关。所以X的熵也可以记做$H(p)=-\sum^{n}{i=1}{p_ilogp_i}$,熵越大，随机变量的不确定性越大。$0\leq H(p)\leq log{n}$.

设随机变量(X,Y)，其联合分布概率为：$P(X=xi,Y=yi)=p{ij},i=1,2,⋯,n;j=1,2,⋯,m$，条件熵(H(Y∣X))表示在已知随机变量X的条件下随机变量Y的不确定性，其定义为X在给定条件下Y的条件概率分布的熵对X的数学期望: $H(Y|X) = \sum^{n}{i=1}p_iH(Y|X=x_i)，p_i = P(X=x_i),i=1,2,\cdots ,n$。当熵和条件熵由数据估计的到，称之为经验熵和经验条件熵。给定数据集D和特征A，经验熵H(D)表示对数据集进行分类的不确定性，经验条件熵H(D|A)表示在特征A给定的条件下，对数据集D进行分类的不确定性。则其差值为信息增益。

信息增益information gain:表示由于特征A而使得数据集D的分类的不确定性减少的程度。定义为:$g(D,A) = H(D) - H(D|A)$。信息增益准则的特征选择方法是：对数据集D，计算每个特征的信息增益，选择信息增益最大的特征。（相对训练数据集而言，没有绝对意义，经验熵大则信息增益大）
信息增益比information gain ratio:$g_R(D,A)$定义为特征$A$对训练数据集$D$的信息增益$g(D,A)$与数据集$D$的经验熵$H(D)$之比。$g_R(D,A)=\frac{g(D,A)}{H(D)}$

2.ID3

ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。

具体方法是：从根结点（root node）开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一棵决策树。ID3相当于用极大似然法进行概率模型的选择。

输入：训练数据集$D$，特征集$A$，阈值$\epsilon$；输出：决策树T。

若$D$中所有实例属于同一类$C_k$，则$T$为单结点树，并将类$C_k$作为该结点的类标记，返回$T$；
若$A$为空，则$T$为单结点树，并将$D$中实例数最大的类$C_k$作为该结点的类标记，返回$T$;
否则，计算$A$中各特征对$D$的信息增益，选择信息增益最大的特征$A_g$；
如果$A_g$的信息增益小于阈值$ϵ$，则置$T$为单结点树，并将$D$中实例数最大的类$C_k$作为该结点的类标记，返回$T$；
否则，对$A_g$的每一可能值$a_i$，依$A_g=a_i$将D分割为若干非空子集$D_i$，将$D_i$中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T，返回$T$；
对第$i$个子结点，以$D_i$为训练集，以$A−{A_g}$为特征集，递归地调用步骤(1)~(5)，得到子树$T_i$，返回$T_i$。

3.C4.5

输入：训练数据集$D$，特征集$A$，阈值$\epsilon$；输出：决策树$T$。

若$D$中所有实例属于同一类$C_k$，则$T$为单结点树，并将类$C_k$作为该结点的类标记，返回$T$；
若$A$为空，则$T$为单结点树，并将$D$中实例数最大的类$C_k$作为该结点的类标记，返回$T$;
否则，计算$A$中各特征对$D$的信息增益比，选择信息增益比最大的特征$A_g$；
如果$A_g$的信息增益比小于阈值$ϵ$，则置$T$为单结点树，并将$D$中实例数最大的类$C_k$作为该结点的类标记，返回$T$；
否则，对$A_g$的每一可能值$a_i$，依$A_g=a_i$将D分割为若干非空子集$D_i$，将$D_i$中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T，返回$T$；
对第$i$个子结点，以$D_i$为训练集，以$A−{A_g}$为特征集，递归地调用步骤(1)~(5)，得到子树$T_i$，返回$T_i$。

4.决策树的剪枝

递归产生决策树，对训练数据的分类很准确，但对未知测试数据的分类容易出现过拟合现象，即在学习时过多考虑如何提高训练数据的正确分类，构建出过于复杂的决策树。

剪枝pruning是将已生成的树进行简化的过程。通过极小化决策树整体的损失函数lossingfunction或代价函数costfunction来实现。设树$T$的叶节点个数为$|T|$，$t$是树|$T$的叶节点，该叶节点有$N$个样本点，其中$k$类的样本点有$N_{tk}$个，$k=1,2,\cdots,K$，$H_t(T)$为叶结点$t$上的经验熵，$\alpha \ge 0$为参数，则决策树学习的损失函数可以定义为：

$C\alpha(T) = \sum^{|T|}{t=1}{ N_rH_t(T)+\alpha|T|}$

经验熵表示为:$Ht(T) = -\sum{k}{\frac{N_{tk}}{Nt}}log{\frac{N{tk}}{N_t}}$

在损失函数中，第一项可以表示为：

$C(T) = \sum^{|T|}_{t=1}{N_rHt(T)}=-\sum^{|T|}{t=1}\sum^{K}{k=1}{N{tk}log{\frac{N_{tk}}{N_t}}}$

则损失函数可以表示为：

$C_\alpha(T) = C(T) +\alpha |T|$

$C(T)$表示模型对训练数据的误差，即模型与训练数据的拟合程度，$|T|$表示模型复杂程度，参数$\alpha \ge 0$控制两者之间的影响，较大的$\alpha$促使选择简单模型，等于0意味着只考虑模型与训练数据的拟合程度，不考虑模型的复杂度。剪枝就是当$\alpha$确定时，选择损失函数最小的模型，即损失函数最小的子树，当$\alpha$确定时，子树越大，与训练数据拟合越好，模型复杂度越高。

决策树生成时只考虑了提高信息增益对训练数据进行更好的拟合，生成学习局部的模型。
剪枝则考虑了优化损失函数和减小模型复杂度。剪枝学习整体的模型。

利用损失函数最小原则就是用正则化的极大似然估计进行模型选择。

剪枝算法：

输入：生成算法产生的整个树$T$，参数$\alpha$。

输出：修剪后的子树$T_\alpha$。

计算每个结点的经验熵
递归地从树的叶节点向上回缩。设一组叶节点回缩到其父结点之前与之后的整体数分别为$T_B$和$TA$，其对应的损失函数值分别是$C\alpha(TB)$与$C\alpha(TA)$，如果$C\alpha(TB) \le C\alpha(T_A)$，则进行剪枝，即将父结点变成新的叶结点。（可以用动态规划算法实现）
返回2,直到不能继续为止，得到损失函数最小的子树$T_\alpha$。

5.CART

分类与回归树:Classification and Regression Trees(CART):

CART 算法是在给定输入随机变量 X 条件下输出随机变量 Y 的条件概率分布的学习方法。
CART 算法假设决策树是二叉树，内部节点特征的取值为“是”和“否”。

这样的决策树等价于递归地二分每个特征，将输入空间/特征空间划分为有限个单元，然后在这些单元上确定在输入给定的条件下输出的条件概率分布。

CART 决策树既可以用于分类，也可以用于回归；

对回归树 CART 算法用平方误差最小化准则来选择特征，对分类树用基尼指数最小化准则选择特征，生成二叉树。

回归树的生成（最小二乘回归树生产算法）

输入：训练数据集D；输出：决策树$f(x)$

在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树;

选择最优切分变量$j$与切分点$s$，求解$ \mathop{min}\limits{j,s}[\mathop{min}\limits{c1} \mathop{\sum}\limits{x_i \in R_1(j,s)}(y_i - c1)^2+ \mathop{min}\limits{c2}\mathop{\sum}\limits{x_i \in R_2(j,s)}(y_i - c_2)^2]$

遍历变量$j$，对固定输入切分变量$j$可以找到最优切分点$s$。选择使得上式达到最小值的对

$(j,s)$。
用选定的对$(j,s)$划分区域并决定相应的输入值：

$R_1(j,s) = {\left{ x|x^{(j)} \le s \right}}, R_2(j,s) = {\left{ x|x^{(j)} \gt s \right}}$

$\hat{c}_m = \frac{1}{Nm}\mathop{\sum}\limits{x_i \in R_m(j,s)}{y_i},x \in R_m,m=1,2$
继续对两个区域调用步骤1,2，直到满足停止条件
将输入空间划分为$M$个区域$R_1,R_2,\cdots,R_M$，生成决策树：

$f(x) = \sum_{m=1}^{M}{\hat{c}_m I(x \in R_m)}$

用平均误差$\mathop{\sum}\limits_{x_i \in R_m}{(y_i-f(x))^2}$来表示回归树对训练数据的预测误差。

分类树的生成

分类树用基尼指数选择最优特征，同时决定该特征的最优二值切分点。

基尼指数:分类问题中，假设有$K$个类，样本点属于第$k$类的概率为$p_k$，则概率分布的基尼指数定义为：

$Gini(p) = \sum_{k=1}^{K}{p_k(1-pk)} = 1-\sum{k=1}^{K}{p_k^2}$

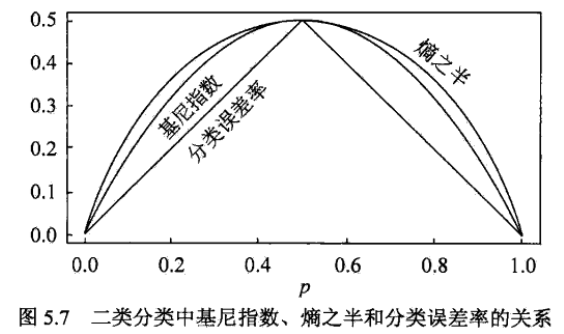
对于二类分类问题，若样本点属于第1类的概率是$p$，则概率分布的基尼指数为：

$Gini(p) = 2p(1-p)$

对于给定的样本集合$D$，基尼指数为：

$Gini(D) = 1-\sum_{k=1}^{K}{( \frac{|C_K|}{|D|})^2}$

$C_k$是$D$中属于第$k$类的样本子集，$K$是类的个数

如果样本集合$D$根据特征A是否取某一可能值$\alpha$被分割成$D_1$和$D_2$两部分，即：

$D_1 = \left{ (x,y) \in D | A(x) = \alpha \right},D_2 = D-D_1$

则在特征$A$的条件下，集合$D$的基尼指数定义为：

$Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$

基尼指数$Gini(D)$表示集合$D$的不确定性，基尼指数$Gini(D,A)$表示经$A=\alpha$分割后集合$D$的不确定性。基尼指数值越大，样本集合的不确定性也就越大。

CART生成算法

输入：训练数据集$D$，停止计算的条件；输出：CART决策树

根据训练数据集，从根节点开始，递归地对每个节点进行以下操作，构建二叉决策树;

设结点的训练数据集为$D$，计算现有特征对该数据集的基尼指数，此时对每一个特征$A$，对其可能取的每个值$a$，根据样本点对$A=\alpha$的测试为“Yes”或“No”将$D$分割成$D_1$和$D_2$两部分，计算$A=\alpha$时的基尼指数。
在所有可能的特征$A$以及它们所有可能的切分点$\alpha$中，选择基尼指数最小的特征，及其对应的切分点作为最优特征与最优切分点，依最优特征与最优切分点，从现结点生成两个子结点，将训练集依特征分配到两个子结点中去。
继续对两个子结点调用步骤1,2，直到满足停止条件
生成CART决策树：

算法停止的条件是结点中的样本个数小于预订阈值，或样本集的基尼指数小于预订阈值，或者没有更多特征。

CART剪枝

1.首先从生成算法产生的决策树$T_0$底端开始不断剪枝，直到$T_0$的根结点，形成一个子树序列$\left{ T_0,T_1,\cdots,T_n\right}$

2.然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树(平方误差或基尼指数最小的决策树)。

CART剪枝算法

输入：CART生成的决策树$T 0$ 输出：最优决策树$T\alpha $

设$k=0$,$T=T_0$
设$\alpha = +\infty$
自下而上地对各内部结点$t$计算$C(T_t)$，$|T_t|$以及$g(t) = \frac{C(t)-C(T_t)}{|T_t|-1}$,$\alpha = min(\alpha,g(t))$

这里$T_t$表示以$t$为根结点的子树，$C(T_t)$是训练数据的预测误差，$|T_t|$是$T_t$的叶结点个数。

自上而下地访问内部结点$t$，如果有$g(t)=\alpha$，进行剪枝，并对叶结点$t$一多数表决法决定其类，得到数$T$
设$k=k+1，\alpha_k=\alpha，T_k=T$
如果$T$不是由根结点单独构成的树，则回到步骤4
采用交叉验证法在子树序列$T_0,T_1,\cdots,Tn$中选取最有子树$T\alpha$

6.Random Forests随机森林

指的是利用多棵树对样本进行训练并预测的一种分类器，由多棵CART构成的。对于每棵树，它们使用的训练集是从总的训练集中有放回采样出来的，这意味着，总的训练集中的有些样本可能多次出现在一棵树的训练集中，也可能从未出现在一棵树的训练集中。在训练每棵树的节点时，使用的特征是从所有特征中按照一定比例随机地无放回的抽取的。

给定训练集S，测试集T，特征维数F。确定参数：使用到的CART的数量t，每棵树的深度d，每个节点使用到的特征数量f，终止条件：节点上最少样本数s，节点上最少的信息增益m。对于第1-t棵树，i=1-t：
从S中有放回的抽取大小和S一样的训练集S(i)，作为根节点的样本，从根节点开始训练
如果当前节点上达到终止条件，则设置当前节点为叶子节点，如果是分类问题，该叶子节点的预测输出为当前节点样本集合中数量最多的那一类c(j)，概率p为c(j)占当前样本集的比例；如果是回归问题，预测输出为当前节点样本集各个样本值的平均值。然后继续训练其他节点。如果当前节点没有达到终止条件，则从F维特征中无放回的随机选取f维特征。利用这f维特征，寻找分类效果最好的一维特征k及其阈值th，当前节点上样本第k维特征小于th的样本被划分到左节点，其余的被划分到右节点。继续训练其他节点。有关分类效果的评判标准在后面会讲。
重复(2)(3)直到所有节点都训练过了或者被标记为叶子节点。
重复(2),(3),(4)直到所有CART都被训练过。

Contents